|
Binary
Numbers that we use everyday have a base of 10 which
means that there are ten numbers used: 0,1,2,3,4,5,6,7,8,
and 9. These 10 numbers without the help of any other
symbols can be rearranged to describe any positive integer.
Binary however, has a base 2 which means that there
are only 2 number used (0 and 1). These too can be arranged
to form any positive integer.
Undoubtably you have seen commercials and backgrounds
of web pages with binary on it. When seeing these commercials
most people know that the 0s and 1s have to do with
computers but have absolutly no idea how and I have
a feeling the people who make the TV ads don't know
how to utilize binary correctly either.
In this tutorial you will learn how to convert base
10 numbers into binary and how to convert binary into
base 10. To make things more simple, I will refer to
base 10 numbers just as "numbers" and base 2 numbers
as binary.
Converting into Binary
Binary conversion is based on powers of 2:
- 2^0 = 1
- 2^1 = 2
- 2^2 = 4
- 2^3 = 8
- 2^4 = 16
- 2^5 = 32
- 2^6 = 64
- 2^7 = 128
We will begin by converting numbers and later it will
be seen that you can convert letters and other characters
into binary. Binary is mainly used with computers to
convert a byte(a number from 0 to 255) into an eight
digit string of 0s and 1s. Get a paper and a pencil
and pick any number between 0 and 255. As you are converting
write the digits and you move along.
|
These are the steps of how you would convert
it into binary:
1.Start with 2^7(128)
- If 128 is greater thanyour number then the
first digit of your binary conversion is 0.
- If 128 is less than your number then the first
digit of your binary conversion is 1. Now subtract
128 from your number. The resulting number will
be used in the following step.
- If 128 is the number then you will use a 1
and all you need to do now is add the rest of
the zeros to make 8 digits. Then your done.
2. Now you will use 2^6(64)
Remember: If you subtracted
128 in the previous step you will use the new resulting
number.
- If 64 is greater than
your number then the second digit of your binary
conversion is 0.
- If 64 is less than your
number then the second digit of you binary conversion
is 1. Now subtract 64 from your number. The
resulting number will be used in the following
step.
- If 64 is the number
then you will use a 1. All the remaining digits
automatically are 0.
3. Now you will use 2^5(32)
Remember: If you subtracted 64 in the previous
step you will use the new resulting number.
- If 32 is greater than
your number then the third digit of your binary
conversion is 0.
- If 32 is less than your
number then the third digit of you binary conversion
is 1. Now subtract 32 from your number. The
resulting number will be used in the following
step.
- If 32 is the number
then you will use a 1. All the remaining digits
are 0.
4. Now you will use 2^4(16)
Remember: If you subtracted 32 in the previous
step you will use the new resulting number.
- If 16 is greater than
your number then the fourth digit of your binary
conversion is 0.
- If 16 is less than your
number then the fourth digit of you binary conversion
is 1. Now subtract 16 from your number. The
resulting number will be used in the following
step.
- If 16 is the number
then you will use a 1. All the remaining digits
are 0.
5. Now you will use 2^3(8)
Remember: If you subtracted 16 in the previous
step you will use the new resulting number.
- If 8 is greater than
your number then the fifth digit of your binary
conversion is 0.
- If 8 is less than your
number then the fifth digit of you binary conversion
is 1. Now subtract 8 from your number. The resulting
number will be used in the following step.
- If 8 is the number then
you will use a 1. All the remaining digits are
0.
6. Now you will use 2^2(4)
Remember: If you subtracted 8 in the previous
step you will use the new resulting number.
- If 4 is greater than
your number then the sixth digit of your binary
conversion is 0.
- If 4 is less than your
number then the sixth digit of you binary conversion
is 1. Now subtract 4 from your number. The resulting
number will be used in the following step.
- If 4 is the number then
you will use a 1. All the remaining digits are
0.
7. Now you will use 2^1(2)
Remember: If you subtracted 4 in the previous
step you will use the new resulting number.
- If 2 is greater than
your number then the seventh digit of your binary
conversion is 0.
- If 2 is less than your
number then the seventh digit of you binary
conversion is 1. Now subtract 2 from your number.
The resulting number will be used in the following
step.
- If 2 is the number then
you will use a 1. All the remaining digits are
0.
8. Now you will use 2^0(1)
Remember: If you subtracted 2 in the previous
step you will use the new resulting number.
- If 1 is greater than
your number then the eighth digit of your binary
conversion is 0.
- If 1 is less than your
number then the eighth digit of you binary conversion
is 1. Now subtract 1 from your number.
- If 1 is the number then
you will use a 1. All the remaining digits are
0.
|
Now lets apply these steps to converting numbers. Since
binary is eight digits long we will use x's as place
holders while converting.
Converting the number 159
1. 128 < 159. So we will use a 1. Subtract
128 from 159 resulting with 31. Currently we have
1xxxxxxx.
2. 64 > 31. So we will use a 0. We now have
10xxxxxx.
3. 32 > 31. So we will use a 0. We now have
100xxxxx.
4. 16 < 31. So we will use a 1. Subtract 16
from 31 resulting in 15. We now have 1001xxxx.
5. 8 < 15. So we will use a 1. Subtract 8 from
15 resulitng in 7. We now have 10011xxx.
6. 4 < 7. So we will use a 1. Subtract 4 from
7 resulting in 3. We now have 100111xx.
7. 2 < 3. So will use a 1. Subtract 2 from 3
resulting in 1. We now have 1001111x.
8. 1 = 1. So we will use a 1. Subtract 1 from
1 resulting in 0. We now have 10011111.
So the binary conversion of 159 is 10011111.
|
Converting the number 202
1. 128 < 202. So we will use a 1. Subtract
128 from 202 resulting with 74. Currently we have
1xxxxxxx.
2. 64 < 74. So we will use a 1. Subtract 64
from 74 resulting in 10. We now have 11xxxxxx.
3. 32 > 10. So we will use a 0. We now have
110xxxxx.
4. 16 > 10. So we will use a 0. We now have
1100xxxx.
5. 8 < 10. So we will use a 1. Subtract 8 from
10 resulitng in 2. We now have 11001xxx.
6. 4 > 2. So we will use a 0. We now have 100110xx.
7. 2 = 2. So will use a 1. Subtract 2 from 2 resulting
in 0. We now have 1100101x.
8. *We have already reached 0 so all the remaining
digits will be 0. We now have 11001010.
So the binary conversion of 202 is 11001010.
|
|
Converting the number 47
1. 128 > 47. So we will use a 0. Currently
we have 0xxxxxxx.
2. 64 > 47. So we will use a 0. We now have
00xxxxxx.
3. 32 < 47. So we will use a 1. Subtract 32
from 47 resulting in 15. We now have 001xxxxx.
4. 16 > 15. So we will use a 0. We now have
0010xxxx.
5. 8 < 15. So we will use a 1. Subtract 8 from
15 resulitng in 7. We now have 00101xxx.
6. 4 < 7. So we will use a 1. Subtract 4 from
7 resulting in 3. We now have 001011xx.
7. 2 < 3. So will use a 1. Subtract 2 from 3
resulting in 1. We now have 0010111x.
8. 1 = 1. So we will use a 1. We now have 00101111
So the binary conversion of 47 is 00101111.
|
Converting out of Binary
Fortunatly for us, converting out of binary is much
simpler than converting into binary.
First, make a table like the one below. In this example
we are going to convert out of 11001010.
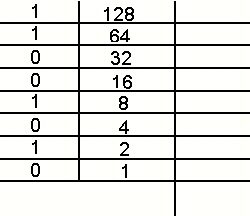As you can see, I have made the binary digit by digit
in the first colomn in the first rows. In the second column
I have listed the powers of 2 in reverse order starting
with 2^7. Now, look at each row and decide whether the
number is a 0 or a 1. If it is a 1 then check the third
box in that row.
After you have check all of the rows with 1's add the
powers of 2s that are in the checked boxes.
128+64+8+2=202. Now if you check the second binary
conversion example you will see that this is the correct
answer.
Ascii
So what practical application does this have? Here you
will see.
|
|
15 = ¤
21 = §
32 = (space)
33 = !
34 = "
35 = #
36 = $
37 = %
38 = &
39 = '
40 = (
41 = )
42 = *
43 = +
44 = ,
45 = -
46 = .
47 = /
48 = 0
49 = 1
50 = 2
51 = 3
52 = 4
53 = 5
54 = 6
55 = 7
56 = 8
57 = 9
58 = :
59 = ;
60 = <
61 = =
62 = >
63 = ?
64 = @
65 = A
66 = B
67 = C
68 = D
69 = E
70 = F
71 = G
72 = H
73 = I
74 = J
75 = K
76 = L
77 = M
78 = N
79 = O
80 = P
81 = Q
82 = R
83 = S
84 = T
85 = U
86 = V
87 = W
88 = X
89 = Y
90 = Z
91 = [
92 = \
93 = ]
94 = ^
95 = _
96 = `
97 = a
98 = b
99 = c
100 = d
101 = e
102 = f
103 = g
104 = h
105 = i
106 = j
107 = k
108 = l
109 = m
110 = n
111 = o
112 = p
113 = q
114 = r
115 = s
116 = t
117 = u
118 = v
119 = w
120 = x
121 = y
122 = z
123 = {
124 = |
125 = }
126 = ~
127 =
128 = €
129 =
130 = ‚
131 = ƒ
132 = „
133 = …
134 = †
135 = ‡
136 = ˆ
137 = ‰
138 = Š
139 = ‹
140 = Œ
141 =
142 = Ž
|
143 =
144 =
145 = ‘
146 = ’
148 = ”
149 = •
150 = –
151 = —
152 = ˜
153 = ™
154 = š
155 = ›
156 = œ
157 =
158 = ž
159 = Ÿ
160 =
161 = ¡
162 = ¢
163 = £
164 = ¤
165 = ¥
166 = ¦
167 = §
168 = ¨
169 = ©
170 = ª
171 = «
172 = ¬
173 =
174 = ®
175 = ¯
176 = °
177 = ±
178 = ²
179 = ³
180 = ´
181 = µ
182 = ¶
183 = ·
184 = ¸
185 = ¹
186 = º
187 = »
188 = ¼
189 = ½
190 = ¾
191 = ¿
192 = À
193 = Á
194 = Â
195 = Ã
196 = Ä
197 = Å
198 = Æ
199 = Ç
200 = È
201 = É
202 = Ê
203 = Ë
204 = Ì
205 = Í
206 = Î
207 = Ï
208 = Ð
209 = Ñ
210 = Ò
211 = Ó
212 = Ô
213 = Õ
214 = Ö
215 = ×
216 = Ø
217 = Ù
218 = Ú
219 = Û
220 = Ü
221 = Ý
222 = Þ
223 = ß
224 = à
225 = á
226 = â
227 = ã
228 = ä
229 = å
230 = æ
231 = ç
232 = è
233 = é
234 = ê
235 = ë
236 = ì
237 = í
238 = î
239 = ï
240 = ð
241 = ñ
242 = ò
243 = ó
244 = ô
245 = õ
246 = ö
247 = ÷
248 = ø
249 = ù
250 = ú
251 = û
252 = ü
253 = ý
254 = þ
255 = ÿ
|
Knowing the numerical value of letters allows you to
convert letters into numbers, then into binary.
For example, if you wanted to know the binary for "T"
you would look at the list and see that it is 84. Then
you can convert 84 into binary.
Now, you can convert words and sentences into binary.
"cat" would be ASCII characters 99, 97, and 116.
Convert these into binary to get 01100011, 01100001, and
01110100.
So "cat" converted into binary would be the combination
of these three: 011000110110000101110100.
To decode 011000110110000101110100 just seperate it back
into groups of 8 then convert back.
You can encode secret messeges with this among other things.
Also, knowing how to convert into and out of binary is
something to brag about. |
